be programmer
유니온 파인드(Union Find) 본문
유니온 파인드는 한 방향 그래프 집합과 다른 방향 그래프 집합을 잇는 알고리즘이다. 여러 노드가 존재할 때 어떤 두개의 노드를 묶고, 그 노드들이 같은 집합에 있는지 확인하는 알고리즘이다.
유니온 파인드를 상호 배타적 집합, 분리 집합이라고 부르기도 한다.
왜 이름이 유니온 파인드인가?
바로 집합을 병합하는 연산(Union) 어떤 원소가 어느 집합에 속해 있는지 찾는 연산(Find)를 수행하기 때문이다.
유니온 파인드 동작 과정
초기 상태
| i | 1 | 2 | 3 | 4 | 5 | 6 |
| p[i] | 1 | 2 | 3 | 4 | 5 | 6 |
위와 같이 모든 원소가 각자 자기만의 값을 가지고 있다.
이때 모든 값이 자기 자신을 가리키도록 만든다.
위의 표는 부모 테이블로 i는 노드 번호를 의미하고, p[i]는 부모 노드 번호를 의미한다.

1과 2를 Union하여 노드를 연결했고, 다음과 같이 표가 변경된다.
표에서는 더 작은 값이 부모가 되도록 설정했다.
| i | 1 | 2 | 3 | 4 | 5 | 6 |
| p[i] | 1 | 1 | 3 | 4 | 5 | 6 |

3을 이으면 다음과 같이 표가 바뀐다.
유의할 점은 여기서는 루트노드가 아닌 부모 노드로 p[i]가 바뀐다. 2와 3을 Union했기 때문이다.
| i | 1 | 2 | 3 | 4 | 5 | 6 |
| p[i] | 1 | 1 | 2 | 4 | 5 | 6 |
1과 3은 그림으로 보면 2를 통해 이어져 있다.
하지만 그림을 통해 보는것이 아닌 표를 통해서만 본다면, 1과 3이 이어져 있음은 쉽게 파악하기 힘들다.
그리고 앞선 방법대로 모든 노드를 이어간다면 아래와 같은 노드 편중 현상이 생길 수 있다.

| i | 1 | 2 | 3 | 4 | 5 | 6 |
| p[i] | 1 | 1 | 2 | 3 | 4 | 5 |
아까 Find 연산은 특정 원소가 어느 집합에 속해 있는지 판단하는 연산을 수행한다고 했다. 1,2,3 집합에서 가장 위에 위치한 집합은 1이다.
따라서 Find(3)연산을 통해 3이 1과 이어져있는지 알 수 있도록 구현해 주어야 하고, 1과 3을 이어주어야 한다.
3의 부모는 2이고, 2의 부모는 1이므로, 재귀함수를 사용하여 1까지 도달하도록 한다.
결과적으로 3의 부모는 1이 됨을 알 수 있고 표와 노드 배치는 이렇게 바뀐다.
| i | 1 | 2 | 3 | 4 | 5 | 6 |
| p[i] | 1 | 1 | 1 | 4 | 5 | 6 |

이렇게 바뀐다면 앞서 설명한 문제인 한쪽으로만 자식이 몰린 노드 편중 현상도 해소되고, 재귀를 통해 탐사하는 트리 속성상 탐사가 오래 걸리는 문제도 해소가 된다.
집합끼리의 합병은 다음과 같다.
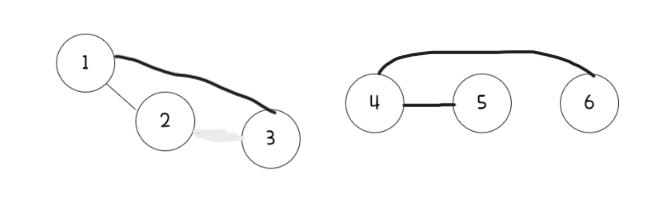
| i | 1 | 2 | 3 | 4 | 5 | 6 |
| p[i] | 1 | 1 | 1 | 4 | 4 | 4 |
123이 연결되어있고, 456이 각자 연결되어있는 유니온 파인드의 트리구조이다.
이때 1번과 4번 집합을 연결하고 싶다면 다음과 같이 집합이 변경된다.
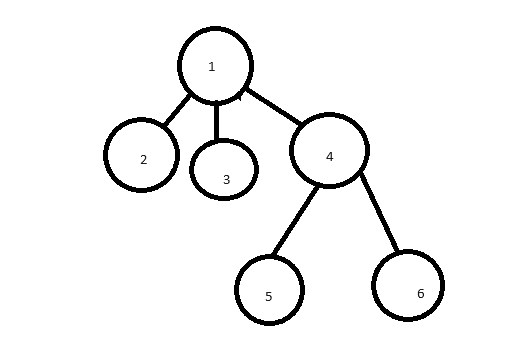
| i | 1 | 2 | 3 | 4 | 5 | 6 |
| p[i] | 1 | 1 | 1 | 1 | 4 | 4 |
1과 4를 이어줬기에 4가 1로 부모가 바뀌고 1과 5와 같은 경우, 4를 통해 간접적으로 이어져 있는 관계이므로 재귀를 통해 탐색된다.
유니온 파인드 코드(JAVA)
class UnionFind{
static int[] arr;
static int find(int x) {
if(arr[x] == x) {
return x;
}
return arr[x] = find(arr[x]);
}
//합병(Union)
static void merge(int x, int y) {
x = find(x);
y = find(y);
if(x == y) return;
arr[y] = x;
}
}
Kruskal 문제를 해당 알고리즘을 사용하여 풀 수 있다.
분리집합을 위주로 사용하는 문제는 다음과 같다.
https://www.acmicpc.net/problem/1717

